동삼이의 노트북
Quantile Regression(분위 회귀) 본문
여기 두 개의 예측이 있다.
- 평균 재정 손실은 4000만원 이다
- 95% 신뢰구간의 재정 손실은 1000만원 ~ 7000만원이고 68% 신뢰구간의 재정 손실은 3000만원 ~ 4000만원이 될 것이다.
위 두개의 예측 중에서 어떤 것이 더 유용하게 쓰일 수 있을까? 당연히 2번일 것이다.
우리는 이전 포스팅을 통해, 혹은 이미 너무 많이 접해서 선형 회귀는 아마 익숙할 것이다. 선형 회귀는 대개 최소자승법(OLS)을 통해 회귀식을 만들고 예측값을 예측한다. 위 1번 예측이 최소자승법을 통해 구해낸 예측 값이다. 그렇다면 두 번째 예측은 무엇일까? 바로 Quantile Regression(분위 회귀)이다. 최소자승법은 쉽게 말해 예측 값 범위 중 평균에 해당하는 값을 구하는 방식이다. 그렇다면 예측 값의 범위 중 중간값이나 분위값에 해당하는 값들은 구할 수가 없는 것일까? 그 정답은 분위 회귀에 있다. 대개 머신러닝 알고리즘은(랜덤포레스트, Gradient Boosting 모델 등) 평균 예측값만 제공한다.
Quantile Regression은 우리가 신뢰 구간에 따른 예측을 구하고 싶거나, 종속 변수의 분포가 이분산성을 띌 때 사용한다.
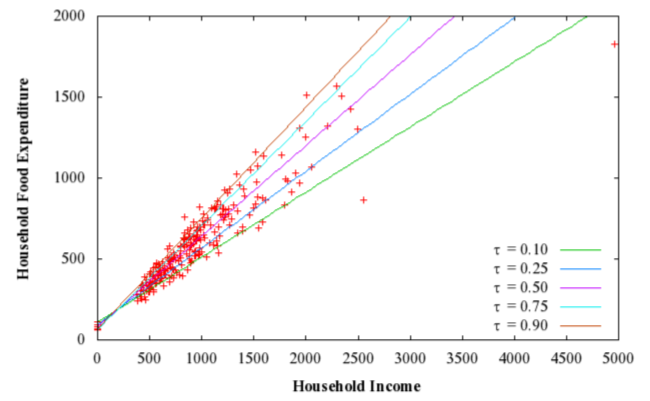
위 그래프는 가구별 음식 소비 지출량을 의미한다. 최소자승법은 평균 예측값만을 반환하는 반면, QR은 5개 분위에 따른 예측값을 나타내고 있다.
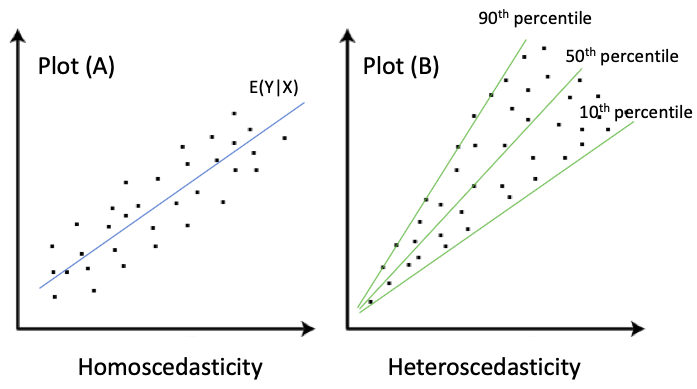
Plot(A)는 X가 증가해도 Y의 분산은 같지만, Plot(B)는 X가 증가하면 Y의 분산도 증가한다. A는 homoscedasticity(등분산성)이고 B는 heteroscedasticity(이분산성)이다. 대개 실제 데이터 셋은 A보다 B의 형태를 띄고 있다. 최소자승법을 사용한 회귀는 등분산성 형태의 데이터를 예측하고 QR은 이분산성 데이터에 더 적합하다.
그렇다면 이 QR을 학습하기 위해 파이썬 실습을 진행해보도록 하자. 사이킷 런에서 제공하는 Boston housing 데이터를 사용하기 위해 라이브러리 및 데이터 셋을 불러온다.

우리는 Boston 지역의 median house value 즉 중간 집값을 구하려고 한다. 즉 MEDV가 타겟 변수가 되는 것이다.
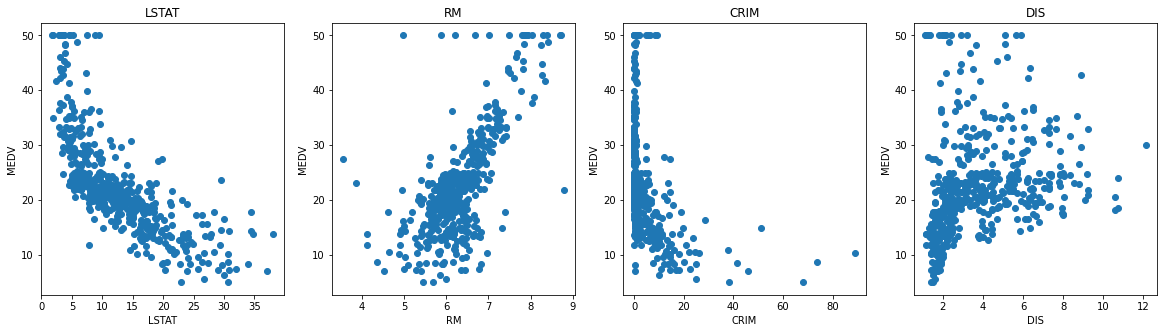
몇가지 변수들과 타겟변수인 MEDV와 관계를 산점도를 통해 나타내 보았다.
간단하게, LSTAT는 인구, RM은 방의 갯수, CRIM은 범죄율, DIS는 보스턴 고용센터까지 거리의 가중 평균을 의미한다.

그 다음, X변수의 스케일링을 위해 위와 같이 코드를 실행하였고, Y변수 역시 스케일링을 진행해주었다
OLS(최소자승법)
앞서 말한것 처럼 최소자승법은 평균을 설명한다.

즉 73% 확률로 구해진 회귀 값이, 예측 값 분포의 평균에 해당하는 값이 되는 것이다.

회귀 계수에 따라 중요도를 시각화하면 위와 같다. LSTAT가 평균을 구하는데에 가장 큰 영향을 미치고 그다음 RAD, DIS가 온다.
Quantile Regression
위의 최소자승법의 회귀에서는 X와 Y 관계의 부분적인 모습만 보여준다. 만약 우리가 y의 분포 중 다양한 부분의 관계에 관심이 있다면 최소자승법은 그것을 표현하기는 힘들다. 예측된 Y값의 1%, 5%, 50%, 95%, 99% 분위 값에 관심이 있다면 QR을 통해 이를 확인할 수 있다.
위 다섯 개 분위의 회귀를 구하려면 5개의 QR이 필요하다. 5개 분위에 해당하는 회귀가 모두 다른 모델이기 때문에, 회귀 계수 또한 전부 상이할 것이다.
quantiles = [0.01, 0.05, 0.50, 0.95 , 0.99]
def Qreg(q):
mod = Q_reg.QuantReg(Y_train, X_train).fit(q=q)
coefs = pd.DataFrame()
coefs['param'] = mod.params
coefs = pd.concat([coefs,mod.conf_int()],axis=1)
coefs['q'] = q
coefs.columns = ['beta','beta_lower','beta_upper','quantile']
pred = pd.Series(mod.predict(X_test).round(2))
return coefs, pred
Qreg_coefs = pd.DataFrame()
Qreg_actual_pred = pd.DataFrame()
for q in quantiles:
coefs, pred = Qreg(q)
Qreg_coefs = pd.concat([Qreg_coefs,coefs])
Qreg_actual_pred = pd.concat([Qreg_actual_pred,pred],axis=1)
Qreg_actual_pred.columns=quantiles
Qreg_actual_pred['actual'] = Y_test
Qreg_actual_pred['interval'] = Qreg_actual_pred[0.99] - Qreg_actual_pred[0.01]
Qreg_actual_pred = Qreg_actual_pred.sort_values('interval')
Qreg_actual_pred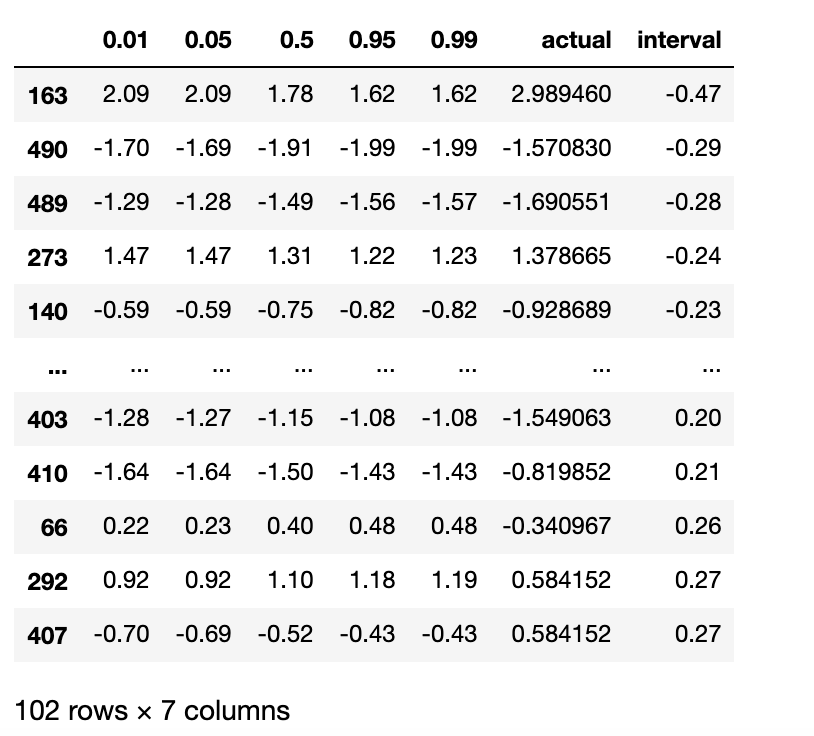
위 코드에서, 우리는 5개 분위를 확인하고 싶었기 때문에 0.01, 0.05, 0.5, 0.95, 0.99 라는 값을 지닌 리스트를 저장하였다. 그 후 각 분위에 해당하는 회귀 모델을 생성하는 함수를 선언하였고, 총 분위 수 만큼 5번을 반복하여 모델 학습을 진행하였다. 그리고 미리 분할해둔 test 데이터 셋을 예측에 사용한 결과 아래와 같이 각 분위 별 예측 값이 나오게 된다. actual은 실제 값을 의미한다. 실제 값이 50% 예측값과 유사한 경우도 있고 전혀 다른 경우도 있다.

50% 분위에서 R-squared 값은 0.75이다. 다섯개 분위 회귀모델에서의 계수는 아래와 같이 시각화할 수 있다.
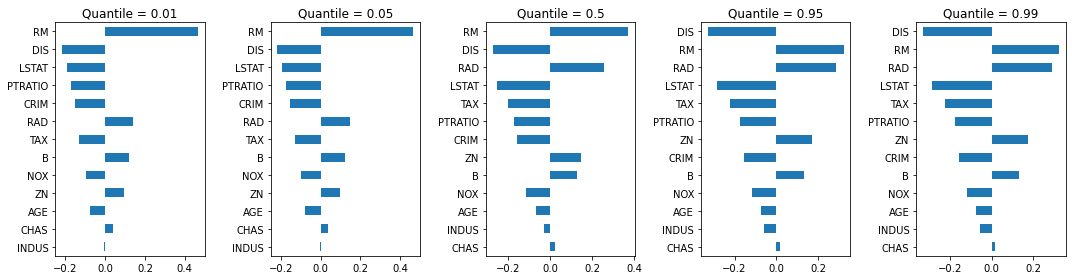
OLS로 회귀를 구했을 때와 QR로 구했을 때의 계수들의 중요도 차이가 있다.
QR은 추정치를 얻기 위해 Least-Absolute-Deviation(LAD)를 사용한다. 이를 설명하기 위해서는 먼저 OLS의 작동 방식부터 시작하여 중간값 회귀(50%)에서 QR에 대한 설명으로 넘어간다. 기존의 선형 회귀는 OLS를 통해 잔차의 합을 최소화하는 식을 구한다. X가 대칭적이라면, 중간값 회귀와 평균 회귀는 거의 같을 것이다.

하지만 LAD를 이용한 회귀 분석에는 OLS와 같은 분석적 해결 방법이 없다. 따라서 LAD를 사용하기 위해서는 아래 식 처럼 추정 오차를 계산하는 Linear Programming 이나 simplex method 같은 기법이 필요하다.

오늘날의 컴퓨팅 환경은 이러한 Linear Programming을 쉽게 할 수 있도록 해주기 때문에 LAD를 사용한 Quantile Regression을 가능하게 한다.
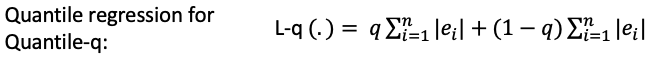
QR은 over-prediction에 대하여 (1-q)|ei|, under-prediction에 대하여 q|ei|의 비대칭 페널티를 곱한 값의 합이 최소화 되는 지점을 구한다. q가 0.5일때, (즉 50% 분위 회귀일 때) 위의 중간값 회귀와 식이 일치해진다.
Quantile GBM
최근의 머신러닝 알고리즘은 Quantile 개념을 포함하여 제공된다. 사이킷 런의 GradientBoostingRegressor는 loss='quantile' 명령어를 통해 분위회귀를 할 수 있게 제공한다. alpha 파라미터에 원하는 분위 수를 입력한다.
from sklearn.ensemble import GradientBoostingRegressor
quantiles = [0.01, 0.05, 0.50, 0.95 , 0.99]
# Get the model and the predictions in (a) - (b)
def GBM(q):
# (a) Modeling
mod = GradientBoostingRegressor(loss='quantile', alpha=q,
n_estimators=500, max_depth=8,
learning_rate=.01, min_samples_leaf=20,
min_samples_split=20)
mod.fit(X_train, Y_train)
# (b) Predictions
pred = pd.Series(mod.predict(X_test).round(2))
return pred, mod
GBM_models=[]
GBM_actual_pred = pd.DataFrame()
for q in quantiles:
pred , model = GBM(q)
GBM_models.append(model)
GBM_actual_pred = pd.concat([GBM_actual_pred,pred],axis=1)
GBM_actual_pred.columns=quantiles
GBM_actual_pred['actual'] = Y_test
GBM_actual_pred['interval'] = GBM_actual_pred[np.max(quantiles)] - GBM_actual_pred[np.min(quantiles)]
GBM_actual_pred = GBM_actual_pred.sort_values('interval')
GBM_actual_predGradientBoostingRegressor 모델을 만들고 데이터를 적합시키고 예측하는 GBM() 이라는 함수를 정의한다. 총 5개 분위수의 모델을 생성해야 하기 때문에 반복을 통해 함수를 실행시켜준다.
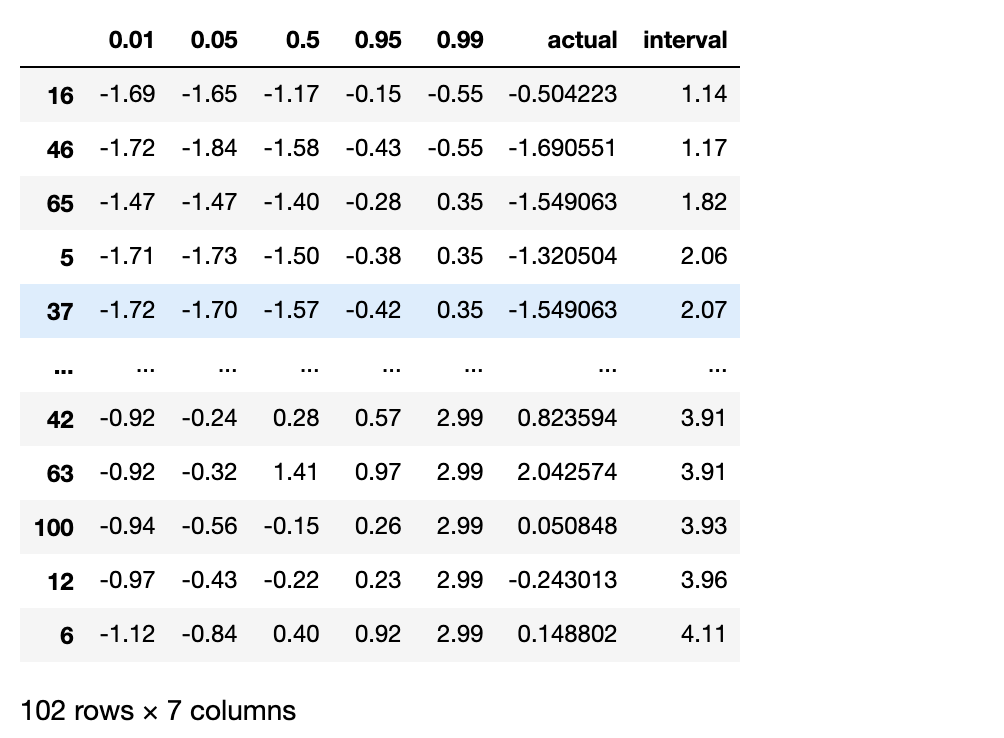
Quantile GBM 모델의 예측 값이다. 위의 Quantile Regression 결과 값과 같은 포맷으로 출력해보았다.

R-squared 값은 기존 QR과 비교하여 0.12 더 높은 값이 나온 것을 확인할 수 있었다.
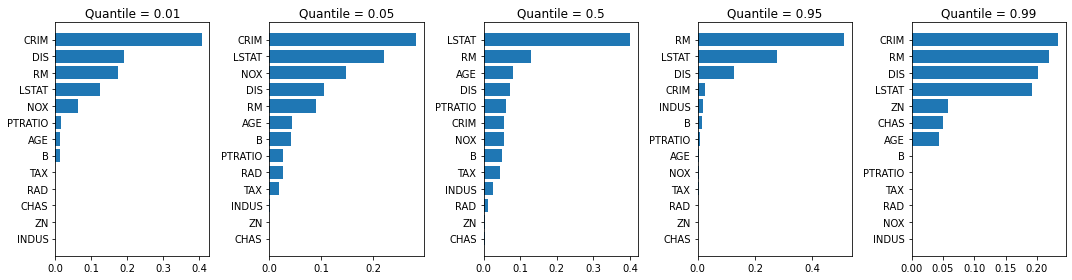
각 분위 GBM 별 feature importances를 구하여 시각화 해보았다. 50% 분위 모델은 LSTAT이 가장 중요한 변수라고 나오는 반면 그 외 분위 모델에서는 각각 다른 변수가 중요도를 차지하고 있다.
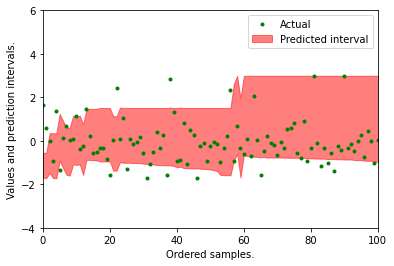
0.01 분위 값과 0.99 분위 값 사이에 거의 대부분의 실제 값이 속해있는 것을 확인 할 수 있다. 위 처럼 시각적으로 얼마나 실제 값들이 예측 구간내에 포함되어 있는지 볼 수 있지만 수식을 통해 수치로도 확인할 수 있다.

1%와 99% 사이의 예측 구간에 실제 값이 포함되어 있는 비율은 96%이다.
Quantile Random Forests
일반적인 랜덤포레스트 모델은 타겟 변수의 정확한 평균 값을 예측해낸다. 하지만 Nicolai Meinshausen가 정의한 타겟 변수의 완전한 분포를 예측해내는 랜덤포레스트를 통해 분위 별 예측 값을 구해낼 수 있게 되었다. 일반적인 랜덤 포레스트는 각각의 의사결정나무의 타겟변수의 평균 값을 계산한다. 만약 각각의 잎(leaf)에서의 모든 값을 기록하고 있다면 분위별 예측 값 또한 구할 수 있을 것이다. 만약 100개의 의사결정나무가 있다고 가정하면, 총 100개의 예측 값이 나올 것이다. 기존의 랜덤포레스트는 이 100개 값의 평균 값을 예측 값으로 반환하겠지만, 우리는 이 100개 값을 전체 분포로 변환하여 분위 예측을 할 수 있을 것이다.

위 코드는 200개의 의사결정나무를 가진 랜덤 포레스트 모델을 생성하여 학습시킨 뒤, 각각의 나무의 예측 값을 하나의 컬럼에 저장하여 나타낸 것이다. 따라서 컬럼의 수가 200개인 데이터프레임이 출력되는 것이다. 200개의 컬럼을 정렬한 뒤 분포 값을 계산하면 분위에 해당하는 값을 구할 수 있게 된다.


위는 pandas의 quantile 메소드를 사용하여 각 분위수에 해당하는 컬럼 값을 찾아낸 것이다.

R-squared 는 위에서 구한 Quantile GBM모델보다 약간 낮지만 QR이나 OLS 모델 보다는 높은 점수를 띄고 있다. 또한 1%와 99% 예측구간 사이에 해당하는 값의 비율은 95%로 GBM 모델보다 약간 낮은 95%로 나타나는 것을 알 수 있다.
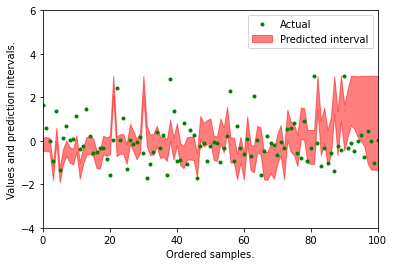
Quantile 랜덤포레스트의 예측 구간은 Quantile GBM 보다 좁지만 보다 과적합되어 구간이 치솟는 것을 알 수 있었다.
'Machine Learning' 카테고리의 다른 글
| 서포트 벡터 머신 (Support Vector Machine) (1) (0) | 2020.12.23 |
|---|---|
| 소프트맥스 회귀(Softmax Regression) (0) | 2020.12.11 |
| 로지스틱 회귀 (logistic regression) (0) | 2020.12.10 |
| 규제가 있는 회귀 - 릿지, 라쏘, 엘라스틱 넷 (0) | 2020.12.08 |
| 선형 회귀 모델 (Linear regression model) (3) - 다항 회귀 (0) | 2020.12.02 |




